Ihr habt sicherlich bemerkt, dass Geocaching in den letzten Jahren einen regelrechten Boom erfahren hat. Es wurden immer mehr Geocacher und irgendwie wollte es nicht stoppen. Deshalb habe ich mich einmal genauer mit dem Phänomen beschäftigt und die Mitgliederzahlen mathematisch betrachtet. Dazu habe ich zunächst Daten gesammelt: die Anzahl der Mitglieder zu verschiedenen Zeitpunkten. Wie sammelt man die Daten? Jedes Mitglied hat ein Anmeldedatum und eine Member-ID. Diese kann man nur indirekt herausfinden, indem man z.B. auf „See the Forum Posts for this User“ klickt und dann in die Adresszeile schaut. Die Member ID wird fortlaufend nummeriert, gibt also an, das wievielte Mitglied man ist. Auf diese Daten wird dann eine mathematische Methode, die „Methode der kleinsten Fehlerquadrate“ genannt wird, angewandt. Man gibt sich einen funktionalen Zusammenhang vor und schaut, bei welchem Parametern der Fehler zu den Daten am kleinsten wird. Mathematisch genauer: Es seien Daten x_i und y_i gegeben. Man gibt sich eine Funktion f(x_i) vor und versucht, den Ausdruck

sum_{i=0}^n | f(x_i)-y_i|^2    (Summe von i=0 bis n von dem Betrag von f(x_i)-y_i zum Quadrat)

zu minimieren, indem man optimale Parameter in der Funktionsdefinition findet. Ich habe als Ansatzfunktion vier verschiedene Arten verwendet und dabei die Fehler verglichen.

Zunächst einmal die (fast) einfachste Funktion, die man kennt: die lineare Funktion f(x)=a*x+b. Die Methode liefert dabei folgendes Ergebnis

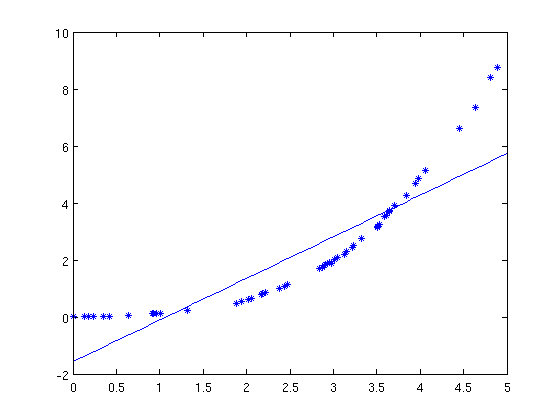Die x-Achse stellt dabei die Tage in 1000 dar, die y-Achse beschreibt die Anzahl der Mitglieder in Millionen. Wie zu erkennen ist, ist dies keine gute Approximation. Der Fehler (also das, was oben minimiert werden sollte), liegt bei 54.7976.

Die nächste Funktion, die jedem bekannt sein sollte, ist eine quadratische Funktion f(x)=a*x^2+b*x+c. Sie liefert folgendes Ergebnis:

Dies sieht schon wesentlich besser aus. Der Fehler liegt bei 1.7148.

Polynomiale Wachstumsprozesse sind in der Natur jedoch eher selten. Bekannt sind da eher exponentielle Wachstumsprozesse, welche durch Funktionen der Form f(x)=a*exp(b*x)+c beschrieben werden. Auch diese Funktion habe ich auf meine Daten angewandt und ich erhalte

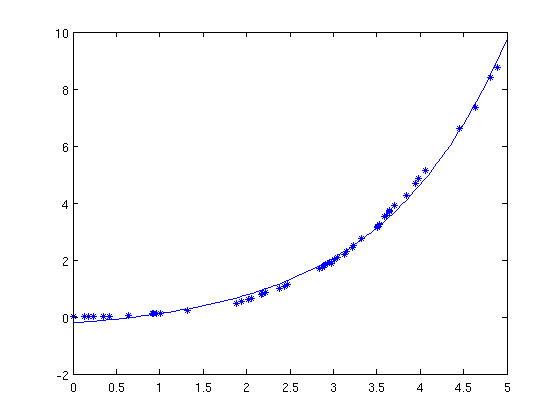Der Fehler liegt bei diesem Ansatz nur noch bei 1.0534. Aber ist dieser Ansatz wirklich realistisch? Wächst die „Geocachingbevölkerung“ immer mehr? Eher nicht. Durch irgendwelche Dinge sind solche Wachstumsprozesse häufig beschränkt, wie z.B. eine Zimmerpflanze durch die Deckenhöhe. Dazu gibt es das sogenannte logistische Wachstum. Die Ansatzfunktion dafür lautet f(x)=a/(1+exp(b-c*x)). Das Ergebnis:

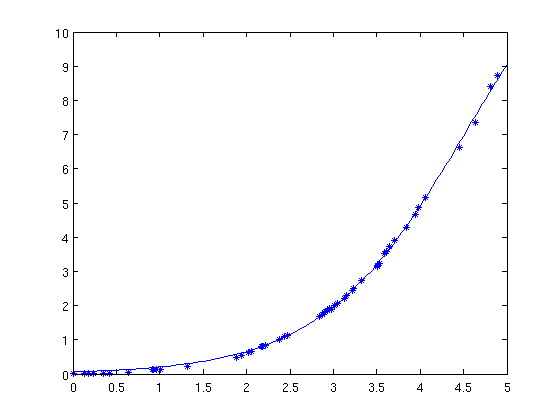Und tatsächlich: der Fehler bei diesem Ansatz liegt hier nur noch bei 0.2241. Das Modell des logistischen Wachstums scheint der Realität am nächsten zu kommen. Und nicht nur das: Aufgrund dieser Approximation könnte man eine Vorhersage treffen, wieviele Geocacher es maximal geben wird. Meine Berechnungen haben ungefähr 14.3 Millionen Mitglieder ergeben. Diese Zahl würde nie erreicht werden, sie stellt eine obere Grenze dar. Man kann aber schätzen, dass ca. im Jahre 2021 14 Millionen Menschen bei geocaching.com angemeldet sein werden. Dies sind natürlich nur Vermutungen. Keiner kann sagen, ob es sich tatsächlich wie diese Funktion verhält. Wenn man noch 2 Jahre wartet, kann man sicherlich schon viel besser bestimmen, ob die Kurve bereits wieder abflacht oder weiter wächst.